ข้อสอบเตรียมทหาร ข้อสอบนายร้อย จปร.
ดาวน์โหลด ข้อสอบเตรียมทหาร.pdf ฟรี
วิชาคณิตศาสตร์ พ.ศ. 2547
ขอร้องว่าอย่าโหลดแล้วเอาไปพิมพ์เพื่อจำหน่ายให้คนอื่นนะครับ แชร์ให้คนอื่น หรือโหลดไปให้คนอื่นดีกว่าครับ
ฝากกดแชร์ คอมเมนต์เพื่อเป็นกำลังใจด้วนะครับ
ผิดพลาดประการใดหรือไม่เหมาะสมฝากแจ้งผม ผ่านทาง คอมเมนต์นะครับ
วิธีการดาวน์โหลดกดที่มุมขวาบนของ PDF นะครับ แล้วมันจะไปยังหน้า เวปแอพ PDF อีกอันหนึ่งแล้วจะมีปุ่มกดให้ดาวน์โหลด(Download)ครับ
ข้อสอบวิชาคณิตศาสตร์ (ข้อ 1-50)
จงเลือกคำตอบที่ถูกต้องเพียงข้อเดียว
1. ถ้า $\frac{a^3+b^3}{a+b}=35$ และ $ab=6$ แล้ว ${(a-b)}^2$ มีค่าเท่ากับเท่าใด
1. 29
2. 31
3. 33
4. 37
5. 41
2. พื้นที่ทั้งหมดของรูปเท่ากับกี่ตารางหน่วย
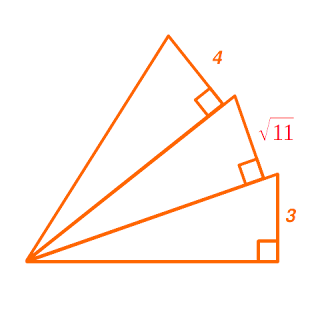 |
| ข้อ 2 |
1. $\frac{30+5\sqrt{11}}{2}$
2. $\frac{34+5\sqrt{11}}{2}$
3. $\frac{36+5\sqrt{11}}{2}$
4. $\frac{38+5\sqrt{11}}{2}$
5. $\frac{40+5\sqrt{11}}{2}$
3. ข้อใดมีค่ามากที่สุดถ้า $a = 2^{45} , b = 3^{36} , c = 4^{27} , d = 5^{18} $ และ $e = 6^9$
1. $a$
2. $b$
3. $c$
4. $d$
5. $e$
4. นายทองมีรายได้ 12,000 บาทต่อเดือน และมีรายจ่ายดังนี้ ค่าเช่าบ้าน $\frac{1}{10}$ ของรายได้ ค่าไฟฟ้า $\frac{1}{6}$ ของค่าเช่าบ้าน และค่าอาหาร $\frac{5}{4}$ ของค่าเช่าบ้าน ส่วนที่เหลือเขานำเงินไปฝากธนาคาร จงหาว่านายทองฝากธนาคารเดือนละกี่บาท
1. 7,700
2. 7,900
3. 8,700
4. 8,900
5. 9,100
5. จากสมการ ${[y^{{2x}^2-3}]}^4 = y^{-4x}$ ถ้า $y \neq 0$ แล้วค่า $x$ เท่ากับเท่าใด
1. 1 หรือ $-\frac{3}{2}$
2. 1 หรือ $-\frac{2}{3}$
3. 1 หรือ $-\frac{1}{3}$
4. 1 หรือ $-\frac{3}{4}$
5. 1 หรือ $-\frac{1}{2}$
6. ซ้อข้าวสารมา 2 ชนิด ราคากิโลกรัมละ 12 บาท และ 8 บาท ถ้านำมาผสมกันในอัตราส่วน 1:1 แล้ว ขายข้าวสารผสมไปในราคากิโลกรัมละ 12 บาท จะได้กำไรกี่เปอร์เซ็นต์
1. 20
2. 24
3. 28
4. 30
5. 32
7. นายดำมองเห็นเครื่องบิน 2 ลำ บินอยู่ในทิศทางเดียวกันและระดับความสูงเท่ากันเป็นมุมเงย $30^\circ$ และ $60^\circ$ ถ้าเครื่องบินทั้ง 2 ลำ บินที่ระดับความสูง 1,500 เมตร เครื่องบินทั้ง 2 ลำ ในขณะนั้นห่างกันกี่เมตร
1. $800\sqrt{3}$
2. $1000\sqrt{3}$
3. $1200\sqrt{3}$
4. $1400\sqrt{3}$
5. $1600\sqrt{3}$
8. ถังน้ำฐานสี่เหลี่ยมจัตุรัสขนาดยาวด้านละ 50 เซนติเมตร และสูง 50 เซนติเมตร บรรจุน้ำไว้ $\frac{3}{10}$ ของปริมาตรถัง ถ้าน้ำรั่วออก 500 ลูกบาศก์เมตรต่อวินาที จงหาว่านานกี่วินาทีน้ำจึงจะเหลือ $\frac{1}{10}$ ของปริมาตร
1. 30
2. 35
3. 40
4. 45
5. 50
9. นางแดงลองสุ่มโดยการโยนเหรียญ 1 อัน 4 ครั้ง จงหาความน่าจะเป็นที่ผลของการโยนเหรียญของนางแดงออกหัวตั้งแต่ 2 ครั้งขึ้นไป
1. $\frac{5}{16}$
2. $\frac{7}{16}$
3. $\frac{9}{16}$
4. $\frac{11}{16}$
5. $\frac{13}{16}$
10. ทอดลูกเต๋า 2 ลูกพร้อมกัน จงหาความน่าจะเป็นที่จะทอดได้ผลรวมหรือผลต่างของแต้มเป็น 3
1. $\frac{1}{6}$
2. $\frac{2}{9}$
3. $\frac{1}{4}$
4. $\frac{4}{9}$
5. $\frac{1}{3}$
11. จากรูปค่าของ x เท่ากับกี่หน่วย
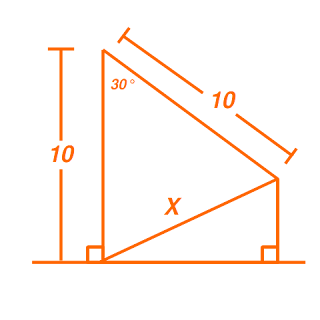 |
| ข้อ 11 |
2. $5\sqrt{\sqrt{3}-1}$
3. $10\sqrt{2-\sqrt{3}}$
4. $10\sqrt{3-\sqrt{2}}$
5. $10\sqrt{\sqrt{2}-1}$
12. ค่าใช้จ่ายในการพิมพ์รูปบนเสื้อ ส่วนหนึ่งคงที่คือค่าทำแท่นพิมพ์ อีกส่วนหนึ่งคือค่าพิมพ์ซึ่งแปรผันตามจำนวนเสื้อที่พิมพ์ ถ้าพิมพ์รูปบนเสื้อ 100 ตัว เสียค่าใช้จ่ายทั้งหมด 10,000 บาท และถ้าพิมพ์ 200 ตัว เสียค่าใช้จ่ายทั้งหมด 18,500 บาท จงหาว่าค่าทำแบบพิมพ์ราคาพี่บาท
1. 500
2. 1000
3. 1500
4. 2000
5. 2500
13. ค่าเฉลี่ยเลขคณิตของข้อมูลชุดหนึ่ง ซึ่งมี m จำนวน เป็น q และค่าเฉลี่ยเลขคณิตของข้อมูลอีกชุดหนึ่งซึ่งมี n จำนวนเป็น p ถ้านำข้อมูลทั้งสองชุดนี้มารวมกันเป็นกลุ่มเดียวกัน จะหาค่าเฉลี่ยเลขคณิตได้ k จงหาว่า p มีค่าเท่าใด
1. $\frac{m}{n}(k-q)+k$
2. $\frac{k(m+n)-q}{n}$
3. $(k+q-1)$
4. $(k-q+1)$
5. $(q-k)+k$
14. ถ้า $\tan{A} = \frac{3}{4}$
1. $2\sin{A} = \frac{6}{5}$
2. $\frac{\cos{A}}{2} = \frac{2}{5}$
3. ${(\sec{A})}^2 = \frac{25}{16}$
4. $3\csc{A} = 5$
5. $5\cot{A} = 3$
15. ระยะทางที่วัตถุตกจากที่สูงแปรผันโดยตรงกับกำลังสองของเวลา ถ้าวัตถุตกจากที่สูงเป็นเวลา 1 วินาที จะตกได้ระยะทาง 5 เมตร ระหว่างวินาทีที่ 5 ถึงวินาทีที่ 7 วัตถุตกได้ระยะทางกี่เมตร
1. 96
2. 108
3. 112
4. 120
5. 144
16. จากสมการ $\frac{2}{3}(6x-2y)<\frac{4}{3}(8x-3y)$ เมื่อ $x$ และ $y>0$ ข้อใดถูกต้อง
1. $5x<2y$
2. $y<x$
3. $5y<2x$
4. $y-3x<0$
5. $2x-y>0$
17. ถ้า $x=\frac{1}{2^k}+\frac{1}{2^{k+1}}+\frac{1}{2^{k+2}}$ และ $y=\frac{1}{2^k}+\frac{1}{2.2^k}+\frac{1}{3.2^k}+\frac{1}{4.2^k}$ เมื่อ $k$ คือจำนวนเต็มบวก
1. $x+\frac{1}{2^{k+3}}<y$
2. $\frac{x}{y}<\frac{2^{k+1}}{2^k}$
3. $y-x<\frac{1}{2^k}$
4. $x+y<2x+\frac{1}{2^{k+2}}$
5. $y=x+\frac{1}{3.2^k}$
18. จากรูป $DE \parallel BA, BC = AC , A\hat{D}C =15^\circ ,A\hat{C}B = 30^\circ ,B\hat{A}C = x^\circ $ และ $A\hat{D}E = y^\circ$ ค่าของ $x$ และ $y$ เท่ากับกี่องศา
 |
| ข้อ 18 |
1. $x=55,y=130$
2. $x=60,y=120$
3. $x=65,y=110$
4. $x=70,y=100$
5. $x=75,y=90$
19. จากรูป $\overline{EF}$ ขนานกับ $\overline{BD}$ ถ้า $AE$ ยาว 4 หน่วย $BD$ ยาว 6 หน่วย และ $CD = EF = BE$ แล้ว $EF$ ยาวกี่หน่วย
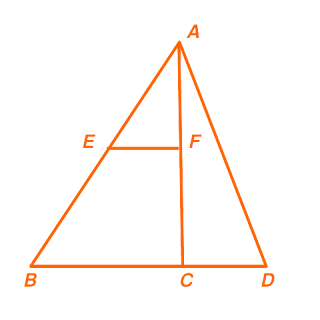 |
| ข้อ 19 |
1. $\sqrt{10}$
2. $\sqrt{10}-1$
3. $2\sqrt{10}-4$
4. $2\sqrt{10}-6$
5. $4\sqrt{10}-8$
20. วงกลมที่มีจุดศูนย์กลางร่วมกัน 2 วงทำให้เกิดวงแหวนซึ่งมีพื้นที่ $46\pi$ ตารางหน่วย คอร์ดของวงกลม ใหญ่ที่สัมผัสวงกลมเล็กยาวกี่หน่วย
1. 12
2. 14
3. 16
4. 18
5. 20
21. จากรูป $OCD = 180^\circ ,COE = 110^\circ , ODE = 55^\circ$ และ $BAD = 28^\circ$ จงหาว่า $BOD$ มีค่าเท่ากับข้อใดต่อไปนี้
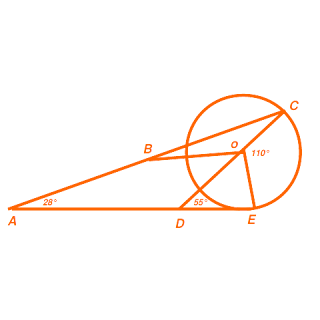 |
| ข้อ 21 |
1. $56^\circ$
2. $54^\circ$
3. $50^\circ$
4. $45^\circ$
5. $42^\circ$
22. ABCD เป็นสี่เหลี่ยมด้านขนาน วงกลมที่ผ่านจุด C ตัด BC,CD และ AC ที่จุด E,F และ G ตามลำดับ ข้อใดต่อไปนี้เป็นสามเหลี่ยมคล้ายกับสามเหลี่ยม EFG
 |
| ข้อ 22 |
1. $\bigtriangleup CGF$
2. $\bigtriangleup CGE$
3. $\bigtriangleup CEF$
4. $\bigtriangleup ACB$
5. $\bigtriangleup ABD$
23. ถังเก็บน้ำมีปั้มสูบน้ำ 3 ตัว ปั้ม ก และ ข สูบน้ำเข้าเต็มถังในเวลา 6 ชั่วโมง และ 12 ชั่วโมง ตามลำดับ ปั้ม ค สูบน้ำออกจากถังมดในเวลา 8 ชั่วโมง เริ่มเปิดปั้ม ก และ ข สูบน้ำเข้าเต็มถังเปล่าพร้อมกันเป็นเวลา 2 ชั่วโมง หลังจากนั้นเริ่มเปิดปั้ม ค เพิ่มขึ้นอีกตัว จงคำนวณว่าจะให้เวลาร่วมกี่ชั่วโมงจึงจะสูบน้ำเข้าเต็มถัง นับเวลาตั้งแต่เริ่มเปิดปั้ม ก และ ข
1. 4
2. 5
3. 6
4. 7
5. 8
24. ในการสอบวิชาคณิตศาสตร์ การตอบข้อสอบแต่ละข้อครูกำหนดว่าถ้าตอบถูกจะได้ 7 คะแนน ถ้าตอบผิดจะหัก 2 คะแนน เลิศชายทำข้อสอบทั้งหมด 18 ข้อ ได้ 36 คะแนน จงหาว่าเลิศชายทำถูกกี่ข้อ
1. 8
2. 9
3. 10
4. 11
5. 12
25. กำหนด $\frac{350}{x-30}-\frac{400}{x}=2$ ถ้า $x_1$ และ $x_2$ เป็นคำตอบของสมการโดยที่ $x_1 > 0$ จงหาว่า $\frac{x_1}{x_2}$ เท่ากับข้อใดต่อไปนี้
1. $-\frac{11}{10}$
2. $-\frac{12}{11}$
3. $-\frac{13}{12}$
4. $-\frac{14}{13}$
5. $-\frac{16}{15}$
26. กรวยกลมสูง 160 เซนติเมตร เส้นรอบวงของฐานกรวยยาว $300\sqrt{\pi}$ เซนติเมตร ปริมาตรของกรวยกลมนี้เท่ากับข้อใด
1. 0.4 ลูกบาศก์เมตร
2. 1.2 ลูกบาศก์เมตร
3. $4.8{\pi}^2$ ลูกบาศก์เมตร
4. $4.8{\pi}^2$ ลูกบาศก์เมตร
5. $9{\pi}^2$ ลูกบาศก์เมตร
27. จากรูป ความยาวของ $\overline{DE}$ เท่ากับกี่หน่วย
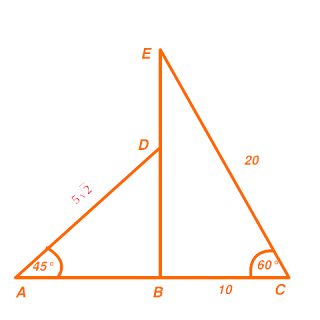 |
| ข้อ 27 |
1. $20\sqrt{3}-5$
2. $\frac{20}{\sqrt{3}}-\frac{5}{\sqrt{2}}$
3. $\frac{10}{\sqrt{3}}-5$
4. $10-5\sqrt{2}$
5. $10\sqrt{3}-5$
28. จากรูปพาราโบลา $y = -4x^2-40x-107$ มีจุดต่ำสุดหรือจุดสูงสุดที่จุดใด
1. จุดสูงสุดที่ (5,7)
2. จุดสูงสุดที่ (-7,5)
3. จุดสูงสุดที่ (-5,-7)
4. จุดสูงสุดที่ (7,-5)
5. จุดสูงสุดที่ (5,-7)
29. $\frac{n^2-16}{n^2-3n-4}\times \frac{n^2-n}{n^2-2n-3}\div\frac{n^2+4n}{n^2+2n+1}$ มีค่าเท่ากับข้อใดต่อไปนี้
1. $\frac{n-1}{n-3}$
2. $\frac{n(n-4)}{n+1}$
3. $\frac{n+1}{n+4}$
4. $\frac{n+1}{n-3}$
5. $\frac{(n+1)(n-4)}{n-2}$
30. ก ขายรถจักรยานให้ ข ได้กำไร 20% ข ขายต่อให้ ค ได้กำไร 10% ถ้า ค ซื้อจาก ข เป็นเงิน 2,772 บาท อยากทราบว่าต้นทุนของจักรยานที่ ก ซื้อมาราคากี่บาท
1. 1,940
2. 1,995
3. 2,000
4. 2,100
5. 2,132
31. อสมการ $11(x-1)-50 \leq 8(2x-3)-16$ มีคำตอบตรงกับข้อใดต่อไปนี้
1. $x \geq -\frac{21}{27}$
2. $x \geq -\frac{21}{19}$
3. $x \geq -\frac{21}{5}$
4. $x \leq -\frac{21}{27}$
5. $x \leq -\frac{21}{5}$
32. ทรงกลมซึ่งมีปริมาตร $\frac{32\pi}{3}$ ลบ.ม จะมีพื้นผิวกรา ตร.ม.
1. 4
2. 8
3. 16
4. $8\pi$
5. $16\pi$
33. ในระยะเวลา 3 วัน คาดคะเนไว้ว่าฝนอาจจะตกหรือไม่ตก โอกาสที่ฝนตกจะตกอย่างน้อย 2 วันเป็นเท่าไร (โจทย์ไม่สมบูรณ์)
1. 4
2. 8
3. 16
4. $8\pi$
5. $16\pi$
34. ในการแข่งขันครั้งหนึ่ง คะแนนสอบเต็ม 100 คะแนน มีผู้เข้าสอบ 50 คน คะแนนสอบที่ได้ของแต่ละคนนำมาสร้างตารางแจกแจงความถี่ได้ดังตารางต่อไปนี้
| คะแนน | ความถี่ |
|---|---|
| 1-25 26-50 51-75 76-100 |
5 10 20 15 |
จงคำนวณหาค่าเฉลี่ยเลขาคณิตของคะแนนสอบครั้งนี้
1. 60.5
2. 61.0
3. 61.5
4. 62.0
5. 62.5
35. กำหนดให้ $6(x+3y+2)-(4x+19y) = 26$
$(8x+15y-15)-4(x+3y) = 23$
ค่าของ $2x+y$ เท่ากับข้อใดต่อไปนี้
1. 14
2. 15
3. 16
4. 17
5. 18
36. กราฟพาราโบลา $y=x^2+1$ ตัดกับกราฟเส้นตรง $x+2y-4=0$ ที่จุด $(x_1,y_1)$ และ $(x_2,y_2)$ ค่าของ $x_1+x_2$ เท่ากับข้อใดต่อไปนี้
1. $-\frac{1}{2}$
2. $-2$
3. $\frac{9}{5}$
4. $\frac{\sqrt{7}-1}{5}$
5. $\frac{\sqrt{17}-1}{5}$
37. ความต้านทาน R ของลวดโลหะเส้นหนึ่งแปรผันโดยตรงกับความยาวของเส้นลวด (L) และแปรผันแบบผกผันกับกำลังสองของรัศมีของหน้าตัด (r) ถ้าลวดเส้นหนึ่งยาว 15 เมตร มีรัศมีของหน้าตัด 0.3 มิลลิเมตรและความต้านทาน 5.0 โอห์ม จงหาว่าลวดชนิดเดียวกันที่มีความยาว 20 เมตร ค่าความต้านทาน 2.4 โอห์ม มีรัศมีของหน้าตัดเท่ากับกี่มิลลิเมตร
1. 0.25
2. 0.50
3. 0.75
4. $\sqrt{0.75}$
5. $\sqrt{0.83}$
38. ในบริเวณหนึ่งมีแบคทีเรียเฉลี่ย $6.4 \times 10^3$ ตัวต่อตารางเซนติเมตร ถ้าพื้นที่ของบริเวณนี้เท่ากับ 2.7 ตารางเมตร จำนวนแบตทีเรียทั้งหมดบนบริเวณนี่เท่ากับกี่ตัว
1. $1.648\times 10^7$
2. $1.648\times 10^8$
3. $1.728\times 10^7$
4. $1.728\times 10^8$
5. $1.728\times 10^9$
39. ชายคนหนึ่งนอนราบอยู่บนตึก A สูง $50\sqrt{3}$ ก้มมองฐานของตึก B เป็นมุม $30^\circ$ กับระดับที่เขานอนอยู่ โดยที่ความสูงของตึก B น้อยกว่าตึก A อยู่ $5\sqrt{61}$ เมตร ถ้าต้องการขึงสายเคเบิ้ลระหว่างมุมตึกด้านบนที่อยู่ใกล้กัน ดังในรูป จะต้องใช้สายเคเบิ้ลที่มีความยาวอย่างน้อยที่สุดกี่เมตร
1. 145
 |
| ข้อ 39 |
2. 155
3. 165
4. 175
5. 185
40. นักบินขับเครื่องบิน บินตามลมระยะ 480 กิโลเมตร ใช้เวลา 2 ชั่วโมง แต่บินทวนลมในระยะเท่าเดิมใช้เวลา 2 ชั่วโมง 40 นาที จงหาว่าอัตราเร็วของเครื่องบินเมื่ออากาศนิ่ง(นักบินเร่งเครื่องเท่าเดิม)เท่ากับกี่กิโลเมตรต่อชั่วโมง
1. 190
2. 200
3. 210
4. 220
5. 230
1. $10^\circ$
2. $15^\circ$
3. $20^\circ$
4. $25^\circ$
5. $30^\circ$
42. ถ้าสมการ $3x^2-28x+30 = k(x^2+19)$ มีคำตอบของสมการเท่ากัน ค่า $k$ เท่ากับข้อใด
1. 2
2. -1
3. 1
4. -2
5. -6
43. จากรูป ถ้า AD = AB = 12 เซนติเมตร และ AC = BD แล้วพื้นที่ของสี่เหลี่ยมจัตุรัสบนด้าน CD เป็นเท่าใด
1. 256 เซนติเมตร
 |
| ข้อ 43 |
2. 288 เซนติเมตร
3. 384 เซนติเมตร
4. 432 เซนติเมตร
5. 576 เซนติเมตร
44. ถ้าสมการ $\frac{2}{x}+\frac{3}{y} = 1\frac{5}{12}$ และ $\frac{3}{x}-\frac{2}{y} = 1$ แล้วค่าของ $\frac{1}{x}+\frac{1}{y}$ เป็นเท่าใด
1. $\frac{9}{14}$
2. $\frac{7}{12}$
3. $\frac{5}{8}$
4. $\frac{5}{6}$
5. $\frac{1}{3}$
45. ผู้ใหญ่ 2 คน กับเด็ก 7 คน ทำงานอย่างหนึ่งเสร็จใน 5 ชั่วโมง ผู้ใหญ่ 3 คน กับเด็ก 5 คน ทำงานอย่างเดียวกันเสร็จใน 4 ชั่วโมง ผู้ใหญ่ 4 คนกับเด็กกี่คน จะทำงานนี้เสร็จในเวลา 2 ชั่วโมง
1. 15
2. 16
3. 18
4. 30
5. 25
46. $3\cot^2{30^\circ}+4\sin^2{60^\circ}-\csc^2{30^\circ}-8\cos^2{60^\circ}-5\tan^2{45^\circ}$ มีค่าเท่าใด
1. 1
2. 2
3. 18
4. -3
5. -5
47. กราฟของสมการในข้อใดแกนสมมาตรเช่นเดียวกับกราฟของสมการ $y=2+2x-x^2$
1. $y=x^2-4x+4$
2. $y=-4x^2-4x+3$
3. $y=x^2-2x-3$
4. $y=-x^2+4x-4$
5. $y=x^2+4x+4$
48. ในการวิ่งแข่งขันระยะทาง 400 เมตร ก. ต่อให้ ข. 20 เมตร แต่กลับแพ้ ข. 10 เมตร ถ้าให้แข่งขันกันในทาง 260 เมตร ก. จะชนะ ข. กี่เมตร
1. 5
2. $5\frac{1}{3}$
3. $5\frac{1}{2}$
4. $6\frac{2}{3}$
5. 10
49. ถ้ามุมภายนอกมุมหนึ่งของรูปหลายเหลี่ยมด้านเท่ารูปหนึ่งเท่ากับ 15 องศา รูปหลายเหลี่ยมนั้นจะมีจำนวนด้านเท่าใด
1. 24
2. 25
3. 30
4. 32
5. 36
50. สมการ $x^2+2x-35 = 0$ มีคำตอบหนึ่งร่วมกับสมการในข้อใด
1. $x^2-x-30 = 0$
2. $x^2-x-42 = 0$
3. $x^2+7x+10 = 0$
4. $x^2+x-56 = 0$
5. $x^2-8x+15 = 0$
ผิดพลาดข้อไหน คอมเมนต์ใต้ล่างด้วยนะครับ ถ้าชอบฝากกดแชร์ด้วยครับ


No comments:
Post a Comment